これは親子で数学の問題を解いていたある日の出来事であり、真実の物語である。
R「パパ、この問題が全然分かんないんだけど。」
始まりはいつもこんな感じです。少しは考えてから聞きに来て欲しい所ではあるんですけど、そこはグッとこらえて先に進むんですね。で、見てみるとこんな問題でした。
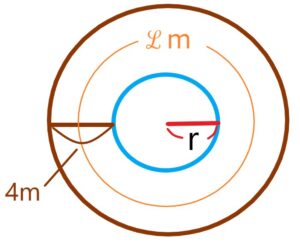
半径rmの円形の池の周囲に、幅4mの道がある。この道の面積をS㎡、この道の真ん中を通る円周の長さを ℒmとすると、S=4ℒ であることを証明しなさい。
R「大体さ、証明して欲しいくせに『しなさい』とか、命令口調なのが気に食わないんだよね。『して頂けますか?』とか、『お願いします』とか言えないのかしら?」
もうね、一事が万事こんな感じ。そこじゃないだろ!ってツッコミたくなるんですけど、これもグッとこらえて、「こーゆー問題の解き方って学校で教わってない?」って聞いてみたんですね。そしたら、
R「たしか、周りの面積を求めてから真ん中を引くって感じだったかなぁ?でもさ、この問題見てたら、池じゃなくてドーナッツに見えてきたんだけど。」

ドーナッツでも池でもええわい!って思いながら、「円の面積はどうやって求めるんだっけ?」って聞いてみたんです。
R「たしか、半径かける直径かけるπとかだったような気が・・」
父「残念。違います。」
R「え、何だっけ?何とかπだってのは覚えてるんだけどなぁ。ってかさ、最近アタシのオッパイの方がママのパイより大きくなってきたと思うんだよね。張りもあるし。」
父「オッパイはどうでもいいから。『そうだよねぇ』とか言ったらママに殴られちゃうし。で、円の面積の求め方を調べて貰っていいですか?」
R「えぇ~っと、半径×半径×πだ。」
父「ですよね。ということはこのドーナッツの半径はいくつ?」
R「えぇ~っと、半径がrと4mだから両方を足して。ん?rと4って足せるんだっけ?」
父「足せますね」
R「じゃあ、『r+4』だ。で、これを2倍するんだっけ?」
父「2乗ですね。」
R「2倍も2乗も同じじゃないの?」
ここで、2倍と2乗の違いを説明する事しばし。で、やっとこさ、全体の面積が求まったんです。その後、池の部分の面積も求められたので、引き算してドーナッツの食べらる部分の面積が求まったんです。次に円周を求める計算に入ったんですけど、ここでも同じようなやり取りを繰り返していて
父「円周はどうやって求めるんでしたっけ?」
R「えぇ~っと、直径の2乗?」
父「ワナワナ・・・ワナワナ・・・(怒りに震える父)」
もうね、ずぅ~っとこんな感じ。でも最後はSが16π+8πrで、ℒが4π+2πrだって答えにたどり着いて、
R「おぉ~、すごい。ちゃんと4倍になってるわ。アタシ、凄い!天才かも」
って。まるで自分一人のお手柄の様にいう訳ですよ。ここまでで20分くらいかな?で、次の問題に取り掛かるんです。その時はまた円の問題だったんですね。
父「円周ってどうやって求めるんでしたっけ?」
R「えぇ~っとね、直径の2乗!」
って。もうね、ニワトリさんですか?ってくらい忘れちゃうんですよ。こりゃ数学の偏差値が30台になるわけだよなぁって思いつつ、老い先短いオヤジの貴重な人生の一日が終わっていく訳です。
まぁ、数学が出来なくても数学の問題にツッコミを入れるセンスがあれば強く生きて行けると信じて、今日も無理やり笑っておこうっと。









コメント